Řešení problému batohu a problému obchodního cestujícího pomocí genetických algoritmů

Problém batohu

Zadání: Máme dáno n předmětů. Pro každý předmět i = 1 ... n máme dánu hmotnost W[i] a cenu P[i]. Je dána kapacita C. Máme najít takový binární vektor x = (x[1] ... x[n]) takový, že (1)

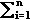x[i] * W[i]

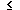C a zároveň je celková cena batohu (2) P(x) =

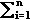x[i] * P[i] je co největší.

Nabízí se hned několik možností, jak tento problém řešit pomocí genetických algoritmů. Ukažme si některé z nich.

Algoritmy A_p[i] - "Penalizační"

V těchto algoritmech reprezentujeme vektory pomocí binárních řetězců délky n. (Tzn. předmět je v batohu právě když x[i] = 1). Kvalitu (fitness) eval(x) spočteme takto: eval(x) =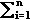

x[i] * P[i] - Pen(x), kde Pen(x) je penalizační funkce.
V našem vyhledávacím prostoru se nacházejí i řetězce, které nesplňují podmínku (1) zadání. Pro tyto řetězce potřebujeme určit nějaké znehodnocení (potřebujeme zmenšit jejich fitness). Toto znehodnocení je reprezentováno penalizační funkcí. Penalizační funkce má hodnotu 0 pro řetězce splňující podmínku (1) zadání. Pro řetězce, které tuto podmínku nesplňují, je kladná. Je mnoho způsobů, jak vypočítávat penalizační funkci. Ukažme si některé možnosti:

logaritmická penalizace (algoritmus A_p[1]): Pen(x) = log₂(1 + r * ( 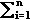x[i] * W[i] -C))
lineární penalizace (algoritmus A_p[2]): r * ( 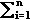x[i] * W[i] -C)
kvadratická penalizace (algoritmus A_p[3]): ( r * ( 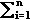x[i] * W[i] -C))²

Ve všech třech případech je r = max_{i = 1 .. n}{P[i]/W[i]}.

Algoritmy A_r[i] - "Opravné"

Reprezentace generace bude v tomto typu algoritmu stejná, jako v A_p[i]. Odlišný bude výpočet kvality řetězce. Stejně jako v předchozím algoritmu nastává situace, kdy řetězec reprezentuje "přeplněný" batoh. Na tyto řetězce voláme opravnou funkci, která některé přebytečné věci z batohu vyhází. Nebo-li bude odebírat předměty z batohu (měnit 1 na 0 na určitých místech řetězce) tak dlouho, dokud nebude splněna podmínka (1) ze zadání (neboli dokud se zbytek do batohu nevejde). Tímto způsobem dostaneme z původního řetězce x řetězec x', který bude reprezentovat platné řešení. Fitness pro řetězec x budeme pak počítat vzorcem eval(x) =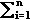

x'[i] * P[i] kde x'[i] je opravený řetězec.
Nastává zde otázka, jestli by se neměli opravované řetězce nahrazovat v generaci opravenými řetězci (má-li x' nahradit x). Orvosh a Davis vyzkoumali, že nejlepší je tuto záměnu dělat s pravděpodobností 5%.
Poslední otázkou, kterou bychom si měli zodpovědět je, v jakém pořadí budou "vyhazovány" předměty z batohu opravným algoritmem. Ukažme si opět více způsobů, jak volit pořadí odebíraných předmětů.

náhodné opravy (A_r[1]): Odebíráme náhodné prvky z batohu.
"hladový" algoritmus (A_r[2]): Všechny předměty, které chceme dát do batohu, setřídíme sestupně podle poměrů cena / hmotnost. Při odebírání vybíráme poslední položku tohoto pořadí (tedy položku s nejnižší hodnotou podílu cena / hmotnost).

Algoritmy A_d[i] - "Dekódovací"

V těchto algoritmech kódujeme problém tak, abychom prohledávali pouze tu část prostoru, která splňuje podmínku (1) ze zadání. Vzdáváme se přitom reprezentace batohu jako binárního řetězce.
Jak tedy postupujeme:
Očíslujeme předměty a vytvoříme si jejich uspořádaný seznam. Mějme tedy třeba 6 různých předmětů a uspořádejme je do následujícího seznamu: (3,4,6,2,1,5). Mějme navíc vektor (4,3,4,1,1,1), který nám kóduje jednu z možností, jak naplnit batoh.
Tento vektor dekódujeme takto: Vybereme položku ve vektoru. Ta nám udává, kterou položku se seznamu máme vybrat. Příslušnou položku v seznamu zapíšeme do výsledku a vyškrtneme ji z kopie seznamu. Pokračujeme další položkou seznamu. Obsah kopie seznamu a výsledku se bude při dekódování našeho vektoru měnit takto:
(3,4,6,2,1,5)
( )

(3,4,6,1,5)
(2)

(3,4,1,5)
(2,6)

(3,4,1)
(2,6,5)

(4,1)
(2,6,5,3)

(1)
(2,6,5,3,4)

( )
(2,6,5,3,4,1) toto je dekódovaný řetězec.
Získané vektor nám udává pořadí, v jakém budou předměty dávány do batohu, dokud bude stačit kapacita batohu.
Při generování nové generace je potřeba ohlídat, abychom generovali pouze vektory které bude možno dekódovat. K tomu je třeba zajistit, aby číslo ve vektoru nebylo nikdy větší než délka zbývajícího seznamu. Tzn. na j-tém místě kódu může být pouze číslo 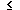n - j + 1, kde n je délka kódu. Díky této vlastnosti získáme při křížení dvou kódů vždy dva nové vektory, které lze dekódovat. Při mutaci musíme příslušné místo kódu měnit tak, aby platila výše zmíněná nerovnost.
Poslední otázkou, kterou musíme při programování vyřešit je, jakým způsobem získáme počáteční seznam pro dekódování. Naznačme si dva různé způsoby:

A_d[1] náhodné dekódovaní: pořadí prvků v seznamu určíme náhodně.
A_d[2] "hladové" dekódování: Podobně jako v A_r[2] spočteme poměr cena / hmotnost a v pořadí sestupném podle tohoto kritéria je vložíme do seznamu.

Výsledky pokusů:

Všechny víše popsané algoritmy byly testovány na těchto datech:
neprovázaná:
W[i] = náhodné číslo od 1 do v
P[i] = náhodné číslo od 1 do v

slabě provázaná:
W[i] = náhodné číslo od 1 do v
P[i] = W[i] + náhodné číslo od -r do r

silně provázaná:
W[i] = náhodné číslo od 1 do v
P[i] = W[i] + r

Dvě různé velikosti batohu C₁ = 2*v, C₂ = 0.5 * 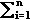W[i]

A_p[i] nedávají dobré výsledky pro batoh kapacity C₁pro všechny typy dat.
Nejlepší výsledek pro kapacitu C₂ dal algoritmus A_p[1] pro všechny typy dat.
"Vítězem kategorie C₁" se jednoznačně stal algoritmus A_r[2].

Problém obchodního cestujícího (TSP)

Zadání: Obchodní cestující má každé město navštívit právě jednou a pak se vrátit do města, ze kterého vycestoval. Naším úkolem je při znalosti ceny cesty mezi jednotlivými městy najít co nejlevnější způsob (pořadí měst), jak tuto cestu provést.

Nejdůležitější při použití genetického algoritmu bude problém, jak cestu zakódovat a jak provést křížení a mutaci. Ukažme si opět několik možností, jak lze úlohu zakódovat.

Sousedská reprezentace (Adjacency Representation)

Města jsou očíslovaná. Cestu budeme kódovat do vektorů délky rovné počtu měst. Číslice na j-tém místě vektoru udává, kam se má vydat obchodník z j-tého města. Cestu přitom vždy začínáme z města číslo 1. Čili například pro 9 měst reprezentuje vektor (2, 4, 8, 3, 9, 7, 1, 5, 6) reprezentuje následující cestu 1-2-4-3-8-5-9-6-7. Ne každý vektor ovšem reprezentuje cestu přes všechna města. Například cesta (3, 1, 2, 4, 5, 6, 7, 8, 9) skončí poměrně brzy. Tyto nepříjemné cykly by se vytvářeli při klasickém použití křížení. Proto je nutné nadefinovat jiné křížení, které obsahuje opravný algoritmus. Možnosti jsou takovéto:

křížení střídáním hran (alternating edges crossover)

(7, 5, 1, 6, 9, 2, 8, 4, 3)

(2, 5, 8, 7, 9, 1, 6, 4, 3)

(7, 8)

křížení střídáním podcest (subtour-chunks crossover)

heuristické křížení

Výhoda sousedské reprezentace spočívá v tom, že nám umožňuje standartní zkoumání pomocí teorie o schematech. Například schema (***3*7***) určuje všechny cesty obsahující hrany (4, 3) a (6, 7).
Tento způsob kódování se nejeví jako nejlepší. Jak křížení střídáním hran tak křížení střídáním podcest má za následek poničení dobrých schemat.

Ordinální reprezentace (Ordinal representation)

Reprezentace podobná jako u algoritmu A_d[i]. Vytvoříme uspořádáný seznam měst. Mějme seznam 6 měst (4, 6, 3, 2, 5, 1) pak vektor (2, 5, 1, 3, 2, 1) bude reprezentovat cestu 6-1-4-5-2-3-6 (konstrukce viz algoritmy A_d[i] v problému batohu). Výhodou této reprezentace je, že funguje běžné křížení a mutace.
Ani tato reprezentace však v TSP nedává dobré výsledky.

Reprezentace cestou (Path representation)

Pravděpodobně nejpřirozenější způsob reprezentace. Nastává zde otázka, jakým způsobem má být definováno křížení, protože klasický způsob křížení zde nefunguje.
Ukažme si některé z možností:

Partially mapped crossover

(x, 2, 3| 1, 8, 7, 6| x, 9)

(x, x, 2| 4, 5, 6, 7| 9, 3).

Zbývající znaky doplníme tak, že na jejich místo dáme ty čísla, které byly starými přepsány v původní sekvenci. Například: při přesunu sekvence do prvního vektoru bylo číslem jedna přepsáno číslo 4. Na starou pozici čísla 1 proto dáme číslo 4. Výsledek operace proto bude tento:

(4, 2, 3| 1, 8, 7, 6| 5, 9)

(1, 5, 2| 4, 5, 6, 7| 9, 3).

Order crossover

(3, 4, 5| 1, 8, 7, 6| 9, 2)

(2, 1, 8| 4, 5, 6, 7| 9, 3).

Původní sekvence prvního řetězce (začínáme za druhým bodem řezu) byla 9-1-2-3-4-5-6-7-8. Při vyplňování dáme za druhý řezový bod 9, nevyskytující se ve vyměněné části. Jednička se ve vyměněné části vyskytuje, takže ji vynecháme. Na poslední místo řetězce tedy dáme číslo 2. Dále pokračujeme na začátku řetezce ve vyměněné části nevyskytující se trojkou atd. Podobně pak pro druhý vektor.

Cycle crossover

(1, 2, 3, 4, 5, 6, 7, 8, 9) a

(4, 1, 2, 8, 7, 6, 9, 3, 5).

Postupovat budeme nyní takto: nejdříve dáme do výsledku první číslo prvního řetězce.

(1, x, x, x, x, x, x, x, x)

(4, 1, 2, 8, 7, 6, 9, 3, 5).

Budeme se nyní snažit, aby všechna čísla ve výsledku byla buďto na stejné pozici v prvním řetězci, nebo aby byla na stejné pozici ve druhém rodičovském řetězci. Jelikož už nemůžeme dát 4 na první pozici, musíme jí dát na pozici čtvrtou. Další krok tedy bude:

(1, x, x, 4, x, x, x, x, x)

(4, 1, 2, 8, 7, 6, 9, 3, 5).

Takto pokračujeme až do stavu, kdy máme

(1, 2, 3, 4, x, x, x, 8, x)

(4, 1, 2, 8, 7, 6, 9, 3, 5).

V této chvíli již algoritmus nevyžaduje žádné přidání číslice z prvního řetězce. Zbytek číslic tedy dodáme z druhého řetězce:

(1, 2, 3, 4, 7, 6, 9, 8, 5)

(4, 1, 2, 8, 7, 6, 9, 3, 5).

Podobnou konstrukci provedeme pro druhý řetězec s tím, že na první pozici dáme číslici z druhého řetězce - tedy 4.

Edge Recombination crossover

Všechny předchozí způsoby ničili v nových řetězcích dosti často hrany, které byly v rodičích. Tento typ křížení se je snaží zachovávat.

Mějme opět dva rodičovské řetězce.

(1, 2, 3, 4, 5, 6, 7, 8, 9) a

(4, 1, 2, 8, 7, 6, 9, 3, 5).

Uděláme si seznam všech hran vedoucích z každého města, které jsou zaznamenány v rodičích:

město 1: 9, 2, 4

město 2: 1, 3, 8

město 3: 2, 4, 9, 5

město 4: 3, 5, 1

město 5: 4, 6, 3

město 6: 5, 7, 9

město 7: 6, 8

město 8: 7, 2, 9

město 9: 8, 1, 6, 3

Cestu začneme ve městě s nejmenším počtem hran. Z přípustných cílů (ještě nenavštívených měst, do kterých se dá z aktuálního města dostat) opět vybíráme město s nejmenším počtem hran. Naše výsledná cesta tedy bude 7-6-5-4-1-2-8-9-3-7. Může nastat situace, že nebudeme mít již hranu do žádného z existujících měst. Pak jej musíme vybrat náhodně. Tato situace se ovšem stává s pravděpodobností 1-1.5%.

V algoritmech používajících Path Representation se používají některé další operátory, které jej vylepší. Algoritmy tuto reprezentaci používající bývají ve vyhledávání řešení TSP vcelku úspěšné.

Všechny informace uvedené na této stránce jsem čerpal z knihy Genetic Algorithms + Data Structures = Evolution Programs od Zbygniewa Michalewicze vydané v roce 1994 nakladatelstvím Springer - Verlag. V této knize najdete mnoho dalších zajímavých informací.
Budete-li mít k tomuto textu jakoukoli připomínku či bude něco nejasného, napište mi

Řešení problému batohu a problému obchodního cestujícího pomocí genetických algoritmů

Problém batohu

Algoritmy Ap[i] - "Penalizační"

Algoritmy Ar[i] - "Opravné"

Algoritmy Ad[i] - "Dekódovací"

Výsledky pokusů:

Problém obchodního cestujícího (TSP)

Sousedská reprezentace (Adjacency Representation)

Ordinální reprezentace (Ordinal representation)

Reprezentace cestou (Path representation)

Algoritmy A_p[i] - "Penalizační"

Algoritmy A_r[i] - "Opravné"

Algoritmy A_d[i] - "Dekódovací"